Comment calculer le périmètre et l'aire d'un octogone régulier

La première chose à faire est de mesurer la longueur de chaque coté du dessin octogonal.

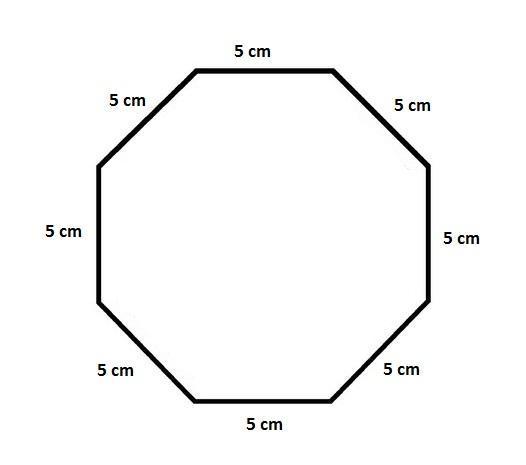
Additionnez les longueurs des cotés de l'octogone afin de déterminer son périmètre. Si les huit cotés sont de longueur identiques ( comme c'est le cas dans l'image), multipliez la longueur d'un coté par le numéro de cotés qui est de 8 pour l'octogone. Par exemple si les huit cotés de l'octogone ont une longueur identique de 5 cm, le périmètre de l’octogone sera égale a 40 cm (5 cm x 8 cotés = 40 cm de périmètre). L'on pourraqit résumer ce calcul par la formule périmètre = longueur d'un coté * nombre de cotés soit p = c * n, ici 40 = 5 x 8

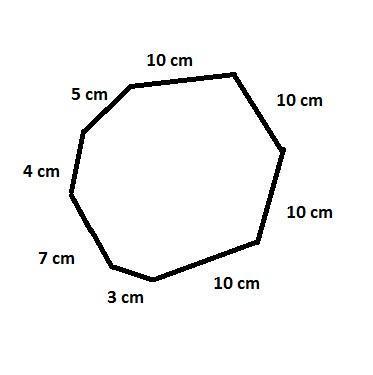
Déterminez le périmètre d'un octogone de cotés non égaux à travers la mesure de chaque coté séparément et l’addition des résultats. Par exemple si le premiers coté est de 5 cm, le deuxième de 4 cm, le troisième de 7 cm, le quatrième de 3 cm, et les cinquième, sixième, septième et huitième cotés sont de 10 cm, le périmètre de l'octogone sera égal a 60 cm (périmètre = 5 + 4 + 7 + 3 + 10 +10 +10 +10 = 60 cm). Ici il n'est pas possible d'appliquer une formule.

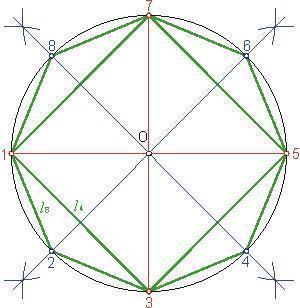
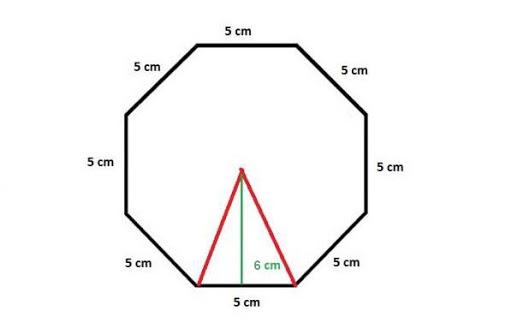
Si nous voulons calculer la superficie ou l'aire d'un octogone régulier comme dans l’étape numéro 2, ce que nous pouvons faire est de diviser l'octogone en 8 triangles égaux, calculer la superficie d'un des triangles puis multiplier par 8. Nous vous rappelons que la superficie d'un triangle se calcule en multipliant la longueur de la base par sa hauteur puis en divisant par 2. Par exemple si chaque coté mesure 5 cm et que la hauteur mesure 6 cm, la superficie du triangle est de 15 cm carrés : ( 5 cm x 6 cm)/ 2 = 15 cm carrés

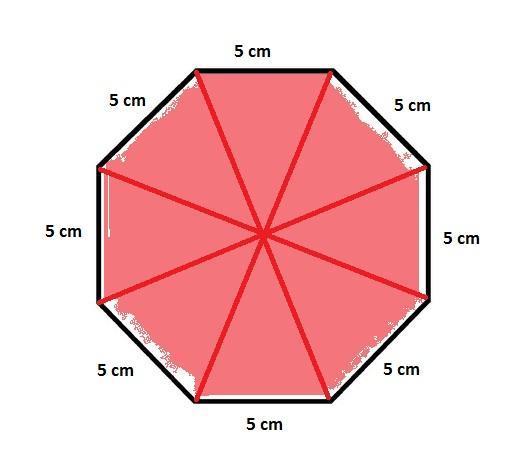
Pour calculer la totalité de la superficie de l'octogone nous devons désormais multiplier l'aire du triangle par 8. Donc Aire = 15 x 8 = 120 cm carrés

La formule est : Aire = n * (b*h )/2.

• n= nombre de triangle
• b= base du triangle
• h= hauteur du triangle

La hauteur du triangle isocèle contenu dans l'octogone est appelé apothème de l'octogone, La base du triangle correspond au coté de l'octogone. Avec ces correspondances nous obtenons la formule suivante :

Aire = (n*c*a)/2

• n = cotés de l'octogone
• c= longueur du coté
• a = apothème

Si vous souhaitez lire plus d'articles semblables à Comment calculer le périmètre et l'aire d'un octogone régulier, nous vous recommandons de consulter la catégorie Formation.

Conseils

• Rappelez-vous qu'à chaque fois que vous calculer des distances, des superficies, des angles etc, il faut donner le résultat dans l'unité correspondante