Comment trouver la hauteur d'un triangle rectangle en utilisant le théorème de Pythagore


La hauteur d'un triangle peut être trouvée de différentes façons, selon le type de triangle et les informations connues sur ses mesures. Les triangles rectangles, qui présentent un angle de 90 degrés, sont les plus faciles à mesurer en utilisant le théorème de Pythagore (si les longueurs des deux côtés sont connues) ou la formule de l'aire (si l'aire et la base sont connues). Les triangles équilatéraux, dont tous les côtés sont de longueur égale, et les triangles isocèles, dont deux côtés sont de longueur égale, peuvent être divisés par la moitié, créant ainsi deux triangles rectangles. Les triangles obliques, dont l'angle intérieur n'est pas égal à 90 degrés, sont plus difficiles à calculer car il faut utiliser la trigonométrie pour trouver leur hauteur.
Dans notre nouvel article Comment trouver la hauteur d'un triangle rectangle en utilisant le théorème de Pythagore, on va calculer la hauteur d'un triangle rectangle en utilisant le théorème de Pythagore.
Vous aurez besoin de:
- Calculatrice scientifique
- Rapporteur
- Règle
Comment calculer la hauteur d'un triangle rectangle
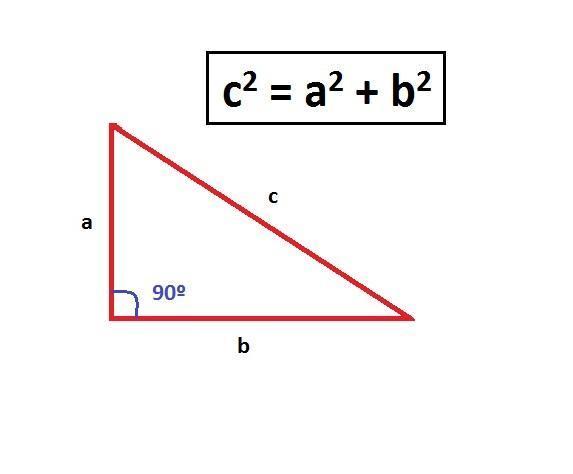
La première chose à faire pour calculer la hauteur d'un triangle consiste à écrire le théorème de Pythagore, c2 = a2 + b2, où c est l'hypoténuse (le côté opposé à l'angle droit).
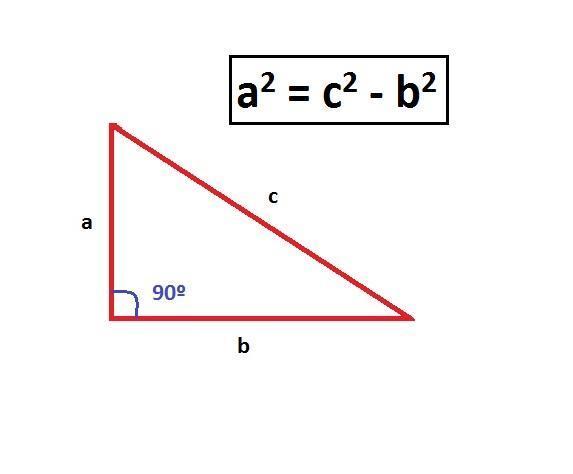
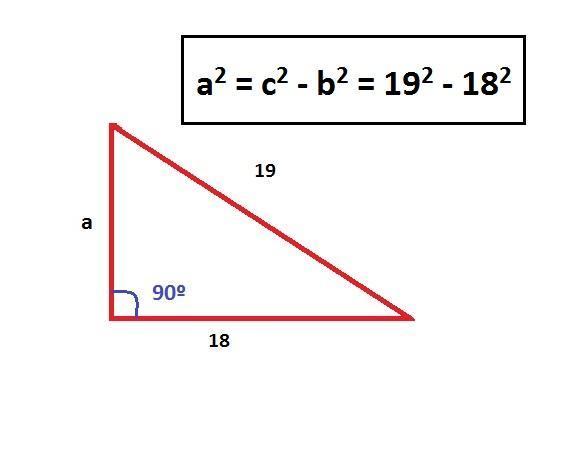
Inversez le théorème pour résoudre a2 , c'est-à-dire a2 = c2 - b2 . Nous voulons trouver la valeur de a qui, comme nous le voyons sur l'image, est la hauteur du triangle.
Rappelez-vous qu'un triangle rectangle est en géométrie un triangle qui possède un angle droit, soit un angle à 90 degrés.
Utilisez les valeurs connues des deux côtés c et b, c'est-à-dire, ici :
- c = 19 cm
- b = 18 cm
Donc on utilise la formule :
a2 = c2 - b2
a2 = 192 - 182
Résolvez ensuite l'équation :
a2 = 361 - 324 = 37 cm
Pour terminer et trouver la valeur réelle de la hauteur du triangle, retranchez la racine carrée des deux côtés a2. Soit
a2 = 37 cm
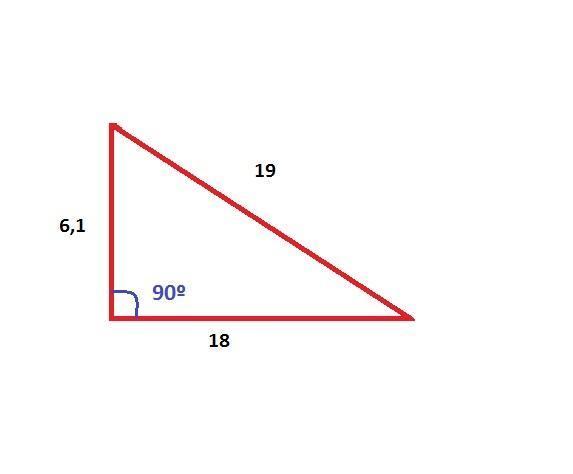
√a2 = 6,1 cm
Nous venons de calculer la hauteur d'un triangle rectangle, qui est de 6,1 cm.
Maintenant que vous savez comment trouver la hauteur d'un triangle rectangle, d'autres articles pourraient vous intéresser :
Si vous souhaitez lire plus d'articles semblables à Comment trouver la hauteur d'un triangle rectangle en utilisant le théorème de Pythagore, nous vous recommandons de consulter la catégorie Formation.
Conseils
- La base peut être n'importe quel côté du triangle.
- La trigonométrie (en utilisant le sinus) peut aussi être appliquée à des triangles rectangles.
- La somme des trois angles d'un triangle est égale à 180 degrés.