Plus grand commun diviseur - Calcul du PGCD

Les mathématiques utilisent différents concepts qui sont complexes à comprendre pour une grande partie de la société, ou du moins qui semblent difficiles à première vue. Le plus grand commun diviseur est un concept mathématique de base qui n'est pas toujours facile à comprendre. Il s'agit d'un nombre clé pour des opérations mathématiques fréquentes, en particulier celles liées aux fractions. Le plus grand commun diviseur est également impliqué dans le raisonnement algébrique. Si vous ne connaissez pas bien le PGCD ou si vous voulez simplement réviser comment le calculer, chez toutCOMMENT, nous vous disons comment trouver le plus grand commun diviseur.
Définition du plus grand commun diviseur
Qu’est-ce que le plus grand commun diviseur ? Avant d’asseoir la définition du plus grand commun diviseur ou la définition du PGCD, retenons ceci : même si les mathématiques ne sont pas votre fort, vous pouvez comprendre la signification et l'origine de ce nombre en regardant son nom. Le plus grand commun diviseur de deux ou plusieurs nombres est le chiffre le plus élevé par lequel ils peuvent tous être divisés sans laisser de reste dans la division, c'est-à-dire des nombres entiers, sans décimales.
Pensez à un ensemble de nombres et passez mentalement en revue les nombres par lesquels vous pourriez diviser chacun d'entre eux de manière à obtenir des divisions exactes, sans aucun reste. Une fois que vous avez fait cela avec tous les nombres, vérifiez si l'un d'entre eux se répète dans tous les nombres. Si c'est le cas, ce nombre serait un commun diviseur, et il peut y en avoir plus d'un, alors quel serait le plus grand commun diviseur ? Ce serait le nombre le plus élevé parmi tous les diviseurs communs possibles. Maintenant, comment calculer le plus grand commun diviseur ?
Comment trouver le plus grand commun diviseur ?
Maintenant que nous avons clarifié la définition du plus grand commun diviseur ou la définition du PGCD, il est temps de savoir comment calculer le plus grand commun diviseur, surtout lorsqu'un exercice mathématique consiste à le trouver dans un ensemble de plusieurs nombres ou entre des nombres très élevés. Alors, il existe deux façons de calculer le PGCD - Plus grand commun diviseur:
Méthode des petits chiffres
La première consiste à trouver tous les diviseurs de chaque nombre et à rechercher simplement celui qui se répète dans tous les cas et à choisir le plus élevé d'entre eux.
Imaginez, par exemple, que vous voulez trouver le plus grand commun diviseur des nombres 10 et 20. Vous devrez diviser chaque chiffre par tous les nombres possibles pour voir lesquels vous donnent un reste nul. Une fois cette opération effectuée, vous obtiendrez le résultat suivant :
Le nombre 10 admet la division exacte (avec reste nul) avec les nombres : 1, 2, 5 et 10.
Le nombre 20 l'admet avec : 1, 2, 4, 5, 10 et 20.
Les diviseurs communs dans ce cas sont : 1, 2, 5 et 10. Parmi eux, quel est le plus grand nombre ? 10, donc 10 est le plus grand commun diviseur.
Il s'agit d'une méthode très simple, mais qui serait très difficile à mettre en œuvre avec des nombres élevés.
Méthode pour les grands nombres : la factorisation
Lorsqu'il s'agit de trouver le plus grand commun diviseur d'un ensemble de deux ou plusieurs grands nombres, la factorisation est la méthode généralement utilisée.
Elle consiste à décomposer chaque nombre en ses facteurs premiers. Une fois cela fait, pour trouver le plus grand commun diviseur, il faut choisir uniquement les facteurs communs (ceux qui se répètent dans tous les chiffres) mais, en plus, uniquement ceux dont l'exposant est le plus petit, et enfin les multiplier entre eux. Le produit obtenu sera le plus grand commun diviseur.
Bien que cette deuxième méthode semble compliquée, elle ne l'est pas pour autant. Pour la rendre plus facile à comprendre, il est préférable de l'examiner à l'aide d'un exemple de plus grand commun diviseur.
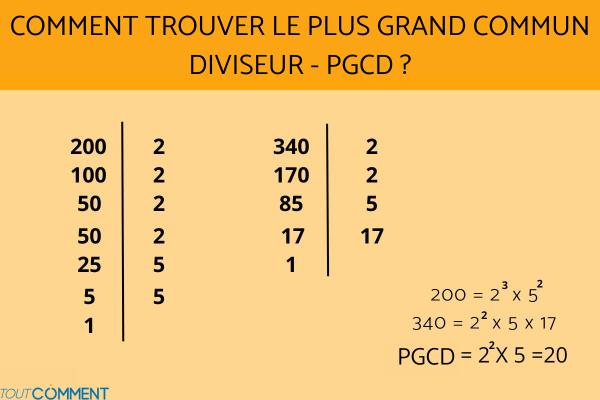
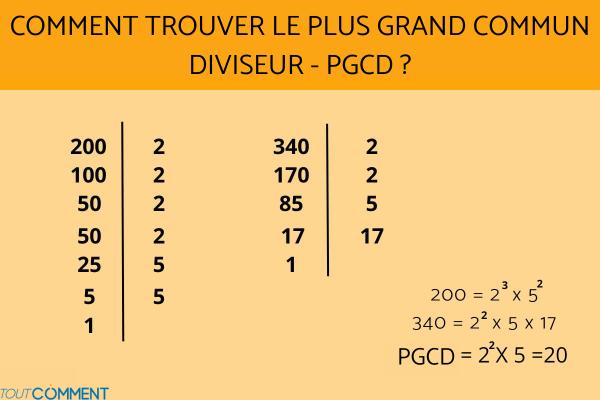
Nous voulons savoir quel est le plus grand commun diviseur des nombres 200 et 340. La décomposition en facteurs premiers serait la suivante :
- 200 : 2 ; 100 : 2 ;50 : 2 ; 25 : 5 ; 5:5 ; 1
- 340:2 ; 170:2 ; 85 : 5 ; 17:17 ; 1
200 = 23 X 52
340 = 22 X 5 X 17
En factorisant, on constate que les deux nombres ont deux communs diviseurs qui sont 2 et 5. Pour obtenir le plus grand commun diviseur, il faudra les multiplier ensemble, mais lequel prendre... celui qui est élevé à la puissance la plus faible. Dans cet exemple, le résultat serait le nombre résultant de la multiplication : 22 X 5 = 20.
Vous pouvez également être intéressé par cet article dans lequel nous vous montrons comment calculer les mètres cubes ou aussi Comment calculer une racine carrée sans calculatrice.
Pourquoi on utilise le PGCD ?
Le plus grand commun diviseur ou le PGCD sert principalement à simplifier les fractions et à en faciliter l'utilisation. Une fois trouvé le plus grand commun diviseur des deux nombres qui composent une fraction, il suffit de diviser à la fois le numérateur et le dénominateur par ce diviseur pour obtenir une fraction simplifiée.
Le plus grand commun diviseur est également utilisé pour calculer un autre chiffre important en mathématiques : le plus petit commun multiple ou le PPCM.
Bien entendu, il peut être essentiel de savoir comment trouver le plus grand commun diviseur pour pouvoir résoudre plus facilement différents problèmes mathématiques, en particulier les calculs qui impliquent de nombreuses divisions avec des nombres différents, mais tous liés et nécessaires pour parvenir à un résultat final.
Plus grand commun diviseur
Maintenant que vous savez comment calculer le plus grand commun diviseur grâce à cet article intitulé Plus grand commun diviseur - Calcul du PGCD, découvrez également le Plus petit commun multiple - Calcul du PPCM.
Si vous souhaitez lire plus d'articles semblables à Plus grand commun diviseur - Calcul du PGCD, nous vous recommandons de consulter la catégorie Formation.





