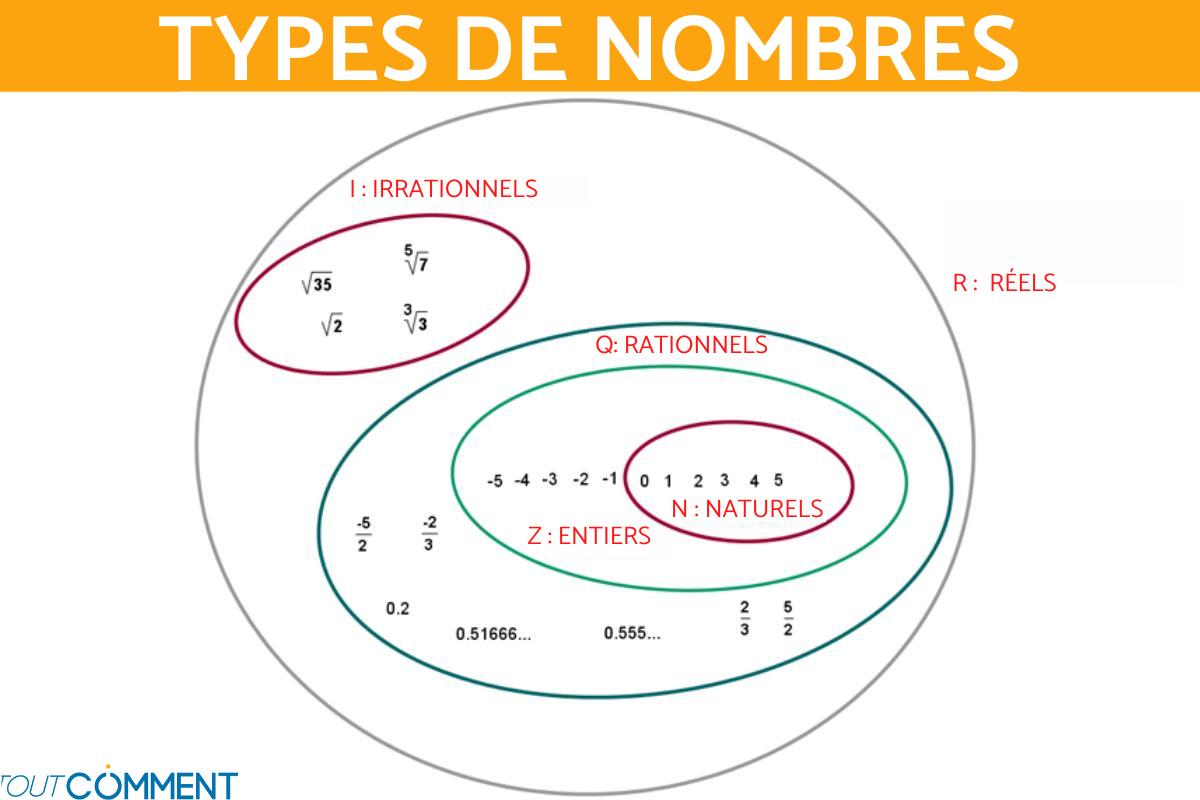
Types de nombres


Les différents types de nombres sont : les nombres naturels, les nombres entiers, les nombres rationnels, les nombres irrationnels ou réels, les nombres décimaux, les nombres réels, les nombres imaginaires, les nombres complexes, les nombres premiers et les nombres entiers de Gauss. Les nombres sont présents dans tous les aspects de la vie quotidienne, car ils nous aident à penser logiquement et à contrôler et grader une trace des choses que nous faisons au jour le jour. Les nombres nous permettent d'accomplir des tâches simples, comme calculer le temps qu'il vous faut pour vous rendre de votre domicile à votre lieu de travail, l'argent dont vous avez besoin pour faire vos courses et le nombre de sacs dont vous avez besoin pour les transporter.
Les nombres sont spécialement utiles pour résoudre des problèmes plus complexes du monde de l'ingénierie et de la science car ils permettent de calculer, par exemple, la charge de combustible nécessaire pour envoyer une fusée dans l'espace ou pour savoir la quantité de camions qu'un entrepôt a besoin pour transporter les commandes de ses clients.
Afin d'en apprendre plus sur les différents types de nombres ainsi que sur leurs caractéristiques respectives, chez toutCOMMENT on vous souhaite une très bonne lecture !
- Nombres naturels
- Nombres entiers
- Nombres rationnels
- Nombres irrationnels
- Nombres décimaux
- Nombres réels
- Nombres imaginaires
- Nombres complexes
- Nombres premiers
- Nombres entiers de Gauss
Nombres naturels
Aussi appelés nombres entiers naturels, les nombres naturels englobent tous les nombres entiers positifs incluant le 0. Ils sont représentés par la lettre N.
Exemples de nombres naturels
N = 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20... etc...
Nombres entiers
Dans les nombres entiers sont inclus tous les nombres positifs et négatifs ainsi que le 0. Un nombre entier est un nombre sans décimale ni fraction. Le 0 est un nombre entier spécial car il n'est ni positif ni négatif et c'est lui qui divise les nombres entiers positifs des négatifs. Ils sont représentés par le lettre Z et voici leur notation : Z : ...-4, -3, -2, -1, 0, 1, 2, 3, 4,...
Par définition, tous les nombres entiers ne sont pas des nombres naturels, mais on peut dire que tous les nombres naturels sont des entiers. Voici quelques exemples d'entiers : -33, -11, 0, 2, 44.
Découvrez comment trouver le plus grand commun diviseur !

Nombres rationnels
Les nombres rationnels sont tous les nombres qui peuvent être exprimés comme le quotient de deux entiers relatifs. Ils peuvent être écrits sous la forme d'une fraction p/q. Ce groupe de nombres comprend les décimales et les fractions. Les nombres rationnels peuvent être présentés sous forme de fraction telles que a|b, (A sur B). A, dans ce cas, est le numérateur et un entier relatif alors que B, qui est le dénominateur, est un entier relatif non nul.
Il est important de noter que tous les nombres naturels et entiers sont rationnels, puisqu'ils peuvent être exprimés sous la forme d'une fraction de dénominateur 1. Par exemple, 3 peut être exprimé sous la forme d'une fraction 3/1.
Voici quelques exemples de nombres rationnels : 1/2, -4/3, 0, 2'99, 77/5.
Nombres irrationnels
Ce sont des nombres qui ne peuvent pas être exprimés sous la forme d'une fraction de deux nombres entiers. Les irrationnels ont des décimales qui ne se répètent jamais et n'ont pas de motif. Ils sont représentés par la lettre Q' (se lit Q prime).
Voici quelques exemples de nombres irrationnels : √2, √6, √11.

Nombres décimaux
Ils comprennent les nombres rationnels et irrationnels. Dans ce cas, les nombres décimaux, qui peuvent être exprimés comme une opération, peuvent être des nombres décimaux finis (par exemple 2/4 = 0,5) ou infinis (par exemple 1/3 = 0,33333...), c'est-à-dire qu'ils peuvent avoir un nombre infini de décimales.
Les nombres décimaux infinis peuvent également être périodiques, c'est-à-dire avoir un motif qui se répète à l'infini (comme 1/3) ou ne pas avoir de motif du tout, comme dans le cas du nombre d'Euler (e) ou du nombre π.
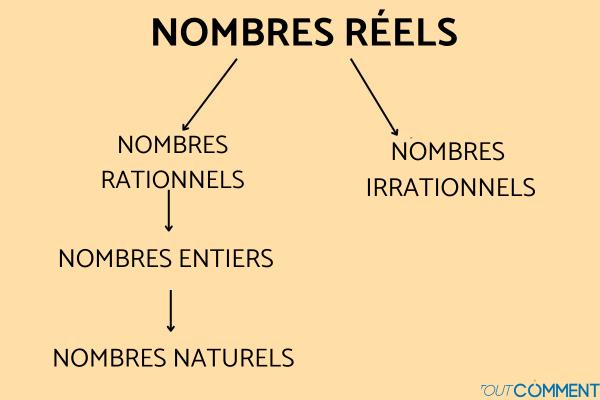
Nombres réels
Ils comprennent tous les nombres que vous pouvez imaginer et rencontrer dans le monde réel, à l'exception des nombres imaginaires. Les nombres réels sont représentés par la lettre R et comprennent tous les nombres rationnels et irrationnels.
L'ensemble des nombres réels peut être représenté par R= Q U Q'. Voici quelques exemples de nombres réels : -7/3,-1,0,0'9,√25.
Nombres imaginaires
Il s'agit de la racine de nombres négatifs. Il n'est pas possible de prendre la racine carrée de nombres négatifs car il n'existe aucun nombre qui, une fois élevé au carré, soit un nombre négatif. Par conséquent, dans ces cas, il faut utiliser des nombres imaginaires. À cette fin, il est établi que i=-1.
Exemple : √-9. On peut l'écrire comme suit : √9*(-1)=√9*√-1. Si vous remplacez i=-1, vous obtenez ce qui suit : sqrt9*√-1= i√9= 3i.
Nombres complexes
Ce sont des nombres dérivés de nombres imaginaires. Ce type de nombre consiste en une paire ordonnée de nombres réels ajoutée à un nombre imaginaire, par exemple : 6 + 3i.

Nombres premiers
Ce sont des nombres qui ne peuvent être divisés exactement que par eux-mêmes et par le chiffre 1. Si un nombre peut être divisé par tout autre nombre que 1 ou lui-même, sans produire de décimales, ce n'est pas un nombre premier.
Par exemple : 7 est un nombre premier parce qu'il ne peut être divisé que par lui-même et par 1 sans produire de décimales. 7/7=1, 7/1=7. Les nombres premiers sont importants dans des domaines tels que la cryptographie. L'une de leurs propriétés est que, jusqu'à présent, il n'existe aucune formule permettant de les prédire. En d'autres termes, il n'est pas possible de prédire l'apparition du prochain nombre premier, ni de les exprimer sous la forme d'une série.
Découvrez dans l'article suivant tout ce qu'il y a à savoir sur les nombres premiers.
Nombres entiers de Gauss
Il s'agit de nombres complexes dont les deux parties de la composition sont des entiers. Ce sont des nombres que l'on n'apprend que dans les études supérieures de mathématiques. Ils font partie d'une structure spéciale appelée anneau euclidien.
Par exemple : 5 + 2i est un entier gaussien.
Si vous aimez les nombres et les chiffres, vous serez passionné par cet article dans lequel on vous propose de découvrir des énigmes mathématiques !
Si vous souhaitez lire plus d'articles semblables à Types de nombres, nous vous recommandons de consulter la catégorie Formation.